SIFT

SIFT(Scale Invariant Feature Transform)

1999년 로우 교수는 지역 특징의 대표격이 되는 SIFT를 발표, 2004년에 확장된 논문을 IJCV학술지에 발표한다.

그림 4-16은 SIFT가 사용하는 스케일 공간으로 피라미드 구조이다. 그림에서는 원래 영상과 반으로 줄인 영상의 두 층만 보여주지만, 실제로는 4x4 정도가 될때까지 계속 줄여나가기 때문에 여러층으로 이뤄진다. SIFT의 스케일 공간은 한 층이 하나의 영상이 아니라 여섯영상의 묶음으로 구성된다. 이들 영상 묶음을 옥타브라 부른다.

여섯 장의 영상은 토대영상을 가우시안으로 스무딩하여 얻는다. 옥타브0에서 옥타브1을 얻는 방법은 기존 옥타브의 토대영상에서 두 픽셀 건너 하나의 픽셀을 얻어 절반 크기의 토대영상을 얻는다. 이후 가우시안 스무딩을 진행한다.

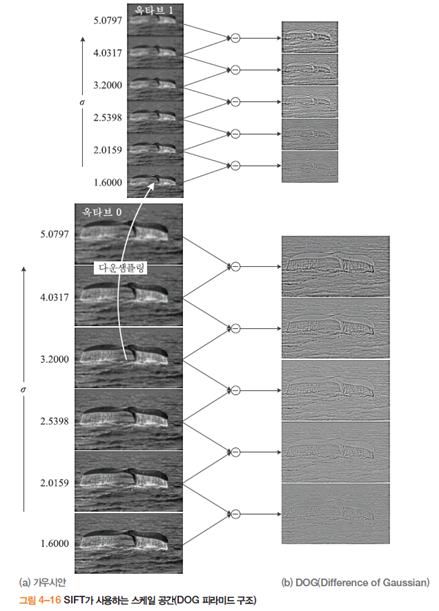
특징점을 찾기위해서 DOG(Difference Of Gaussian)맵을 이용한다. DOG는 정규 라플라시안 식과 유사하지만 옥타브 내의 영상간의 차로 구할 수 있어 계산에 유리하다. DOG피라미드가 완성되면, DOG 옥타브 5개중 양 끝을 제외한 가운데 3개의 DOG영상을 이용하여 극점을 찾는다.

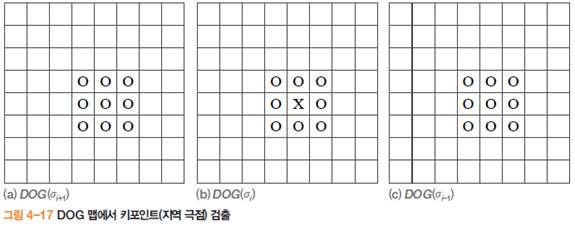
어떠한 점 (그림에서 x표시된 화소)은 자신의 위와 아래에 있는 DOG영상을 같이 살펴보는데, 자신이 26개의 이수점(자신이 속한 DOG영상의 8개 이웃과 위와 아래에 있는 영상의 18개 이웃)에 비해 최소 또는 최대가 되면 극점, 즉 특징점으로 취한다. 이때 임계값보다 작은 극점은 잡음으로 간주하여 버린다. 로우는 이러한 극점을 키포인트라 불렀다.

이렇게 검출된 특징점은 <y,x,o,i>정보를 가진다. o는 옥타브, i는 DOG번호, y,x는 옥타브 o에서늬 좌표이다. 이들 값은 특징점을 중심으로 테일러 확장을 구하고 그것을 기반으로 네개의 값을 미세조정하는 단계를 거친다. 이때 (y,x)는 실수로 표현되는 부분 화소 정확도까지 미세조정한다. (자세한 구현은 논문 참조) 미세조정을 거쳐 특징점 정보가 (y’,x’,o,i’)가 되었다면, (y’, x’)를 옥타브 0에 있는 영상을 위치 (y,x)로 바꾸어야하며, (o,i’)를 스케일값 s로 변환해야한다. 식 (4.21)은 이 일을 위한 식이다.

출처 - Computer Vision