스케일 공간
스케일 공간
스케일에 불변한(scale-invariant) 특징을 찾는 데에 있다. [알고리즘 4-2]는 이러한 생각에 따라 스케일 불변한 특징을 찾는 큰 틀을 설명한다.
- 알고리즘 4-2 다중 스케일 접근 방법
입력 : 영상 f(j,), 0<=j<=M-1, 0<=i<=N-1, 임계값 T
출력 : 특징점 리스트 F
1 f에서 다중 스케일 영상, M={fs0, fs1, fs2, …}를 구성한다. // fsi는 스케일이 si인 영상
2 M에서 3차원 극점을 찾아 특징점 집합 F로 취한다. // 극점 (y,x,s)는 스케일 불변이어야 함.
다중 스케일 영상 구축
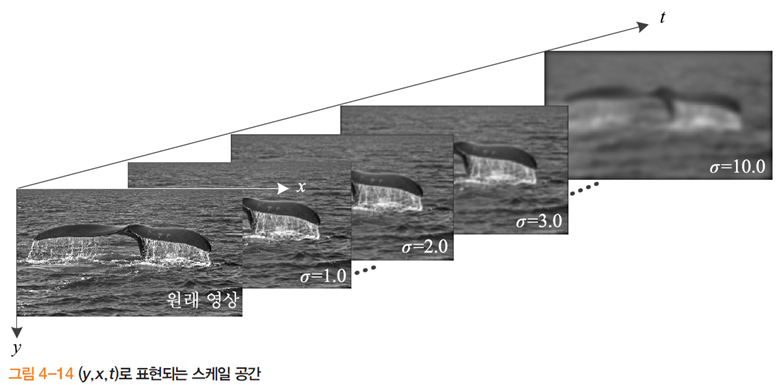
첫 번째 방식은 거리가 멀어지면 물체의 세밀한 내용은 사라지고 윤곽은 점점 흐릿해지는 원리를 이용한다. [그림 4-13(a)]는 \(σ\)를 점점 키워가며 가우시안 마스크로 스무딩 연산을 하여 이런 효과를 모방한다. 두 번째 방식은 [그림 4-13(b)]에서 보는 바와 같이 영상의 해상도를 반씩 줄여나감으로써 피라미드 영상을 구축한다.

[그림 4-14]는 표준편차(standard deviation) \(σ\)의 값을 점점 크게 하여 얻은 일련의 영상을 보여주는데, 이런 영상 집합을 다중 스케일 영상(multi-scale image) 이라고 부른다. 그림에서는 \(σ\)를 1.0씩 증가시켜 얻은 다중 스케일을 보여주는데, 스케일 불변 특징을 검출할 때는 보다 촘촘히 다중 스케일을 구성한다. 한편 이들이 구성하는 3차원 공간, 즉 (y,x,t)공간을 스케일 공간(scale space)이라 부른다. 스케일 공간에서는 분산(variance)을 나타내는 변수 \(t\)를 스케일 매개변수(scale parameter)라 부르며, \(t=σ^2\)이다.
스케일 공간에 있는 영상을 미분하여 얻은 도함수는 매우 유용한 정보를 제공하는데, \(n\)차까지의 도함수를 \(n\)-젯(n-jet)이라 부른다. 이들 도함수는 모두 회전에 공변(covariant)이다. 영상 내에서 물체가 회전하면 이들 값도 그에 따라 달라진다. 이들로부터 회전에 불변한 값들을 정의할 수 있다. 식 (4.16)의 세 가지 측정값은 모두 회전에 불변 이다. 영상 내에서 물체가 회전하더라도 이들 값은 변하지 않는다. \(\textcolor{Black}{ |∇f|=√(d_x^2+d_y^2 )\quad(그레이디언트 크기) }\) \(\textcolor{Black}{ ∇^2 f=d_yy+d_xx\quad(라플라시안)\quad(4.16) }\) \(\textcolor{Black}{ det(H)=d_yy d_xx−d_yx^2\quad(헤시안의 행렬값) }\)
3차원 지역 극점 탐색
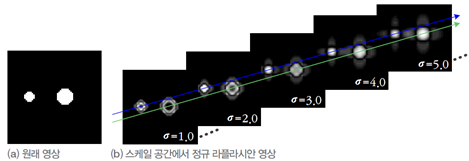
 [그림 4-15(a)] 왼쪽은 지름이 7, 오른쪽은 11인 원형블롭이다.
[그림 4-15(b)]는 다중 스케일 영상에 식 (4.17)의 정규 라플라시엔(normalized Laplacian)을 적용한 결과이다.
정규 라플라시안은 식 (4.16)의 라플라시안에 \(σ2\)을 곱한 식이다. 정규화를 하는 이유는 라플라시안을 구성하는 \(d_yy\) 와 \(d_xx\) 가 \(σ\)가 클수록 작아지기 때문이다. 이러한 현상을 보완하기위해 \(σ^2\)을 곱한다.
\(\textcolor{Black}{
∇_{norm^2} f=σ^2 |d_{yy} (σ)+d_{xx} (σ)|\quad(4.17)
}\)
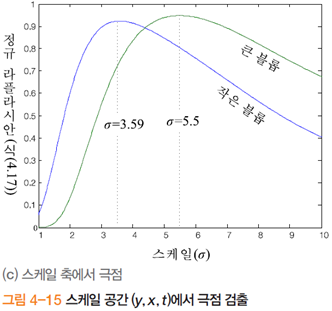
[그림 4-15(c)]는 두 개 블롭의 중심에서 스케일 축(σ 값)에 따라 라플라시안 값의 변화를 보여준다.
[그림 4-15(a)] 왼쪽은 지름이 7, 오른쪽은 11인 원형블롭이다.
[그림 4-15(b)]는 다중 스케일 영상에 식 (4.17)의 정규 라플라시엔(normalized Laplacian)을 적용한 결과이다.
정규 라플라시안은 식 (4.16)의 라플라시안에 \(σ2\)을 곱한 식이다. 정규화를 하는 이유는 라플라시안을 구성하는 \(d_yy\) 와 \(d_xx\) 가 \(σ\)가 클수록 작아지기 때문이다. 이러한 현상을 보완하기위해 \(σ^2\)을 곱한다.
\(\textcolor{Black}{
∇_{norm^2} f=σ^2 |d_{yy} (σ)+d_{xx} (σ)|\quad(4.17)
}\)
[그림 4-15(c)]는 두 개 블롭의 중심에서 스케일 축(σ 값)에 따라 라플라시안 값의 변화를 보여준다.

출처 - Computer Vision