2차 미분을 사용한 방법과 슈산
2차 미분을 사용한 방법
헤시안 행렬 \(\textcolor{Black}{ H=\begin{pmatrix}d_{yy}&&d_{yx}\\d_{yx}&&d_{xx} \end{pmatrix} \quad (4.10) }\)
예를 들어 \(d_yx (σ)\)는 입력 영상 \(f\)를 \(σ\)크기의 가우시안 필터 \(G\)로 컨볼루션한 후, 그 결과영상을 \(y\)방향으로 미분하고 다시 \(x\)방향으로 미분하여 얻은 도함수이다.
\[\textcolor{Black}{ H=\begin{pmatrix}d_{yy}(σ)&&d_{yx}(σ)\\d_{yx}(σ)&&d_{xx}(σ) \end{pmatrix} \quad (4.10) }\]이때 , \(\textcolor{Black}{ d_{st}(σ)=\frac{∂}{∂t} \Big(\frac{∂}{∂s} \big(G(y,x,σ) ∗f(y,x) \big) \Big) }\) , \(s\)와 \(t\)는 \(y\) 또는 \(x\)
-
헤시안 행렬식(determinant) \(\textcolor{Black}{ C=det(H)=d_{yy} (σ) d_{xx} (σ)−d_{yx} (σ)^2 \quad (4.12) }\)
-
가우시안 라플라시안(LOG) \(\textcolor{Black}{ C=∇^2=trace(H)=d_{yy} (σ)+d_{xx} (σ) \quad(4.13) }\)
## 슈산SUSAN(Smallest Univalue SegmentAssimilationg Nucleus)
현재 처리 중인 중심점과 인근 지역의 밝기 값이 얼마나 유사한가를 따져 보고 그 결과에 따라 특징일 가능성을 측정한다.
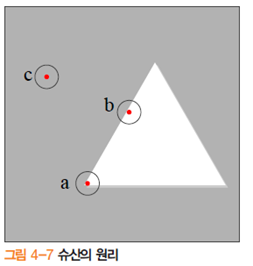
먼저 \(c\)라고 표시된 곳을 살펴보자. 원의 중심이 현재 처리 중인 지점이다. 이 중심점에 원형 마스크를 씌우는데, 중심점과 명암값이 같은(실제로는 유사한) 점으로 구성된 영역을 우산USAN(Univalue Segment Assimilating nucleus)이라 부른다. C의경우 우산의 크기는 마스크 크기의 100%이다. \(b\)의 우산은 50%, \(a\)의 우산은 50% 이하이다.
\(\textcolor{Black}{
usan\_area(r_0)=\sum_rs(r,r_0)
}\)
이때
\(\textcolor{Black}{
s(r,r_0 )=
\begin{cases}
1,|f(r)−f(r_0 )|≤t_1\\
0, 그렇지 않으면
\end{cases}
\quad (4.14)
}\)
우산의 크기 \(usan\_area(r_0)\)를 특징일 가능성을 표현 해 주는 값으로 변환하기 위해 식 (4.15)를 사용한다. 여기에서 \(t_2\)는 또 다른 임계값으로서, 보통 마스크 넓이의 50%로 설정한다. $Q$는 0.75x마스크의 넓이로 설정한다.
\(\textcolor{Black}{
C=
\begin{cases}
q−usan\_area(r_0 ) usan\_area(r_0 )≤t_2\\
0, 그렇지 않으면
\end{cases}
\quad (4.15)
}\)

출처 - Computer Vision