RANSAC

RANSAC (RANdom Sample Consensus)

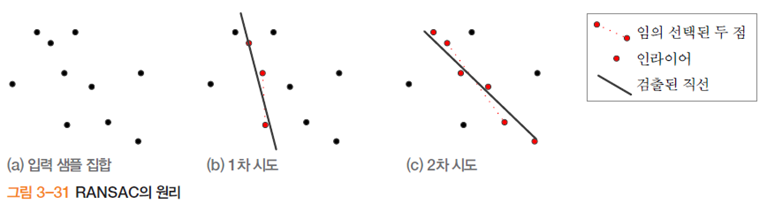
[그림 3-31]은 RANSAC의 원리를 설명한다. 난수를 생성하여 임의로 두 개의 샘플을 선택한다. 그림에서 점선으로 연결된 빨간색 두 점이 선택된 점이다. 이들을 가지고 직선의 방정식, 즉 기울기 a와 절편 b를 계산한다. 초기모델을 추정하는 단계이다. 이제 나머지 샘플들에 대해 이 모델에 적합한, 즉 일직선 상에 있는 점들을 구한다. 이때 약간의 오차를 허용하며, 오차의 범위는 [알고리즘 3-8]에서 t라는 매개변수로 조절한다. 이 점들을 인라이어inlier라 부른다. 나머지는 아웃라이어outlier이다. 인라이어 개수가 충분치 않은 경우 이 모델을 버린다. 충분한 정도는 [알고리즘 3-8]에서 d라는 매개변수로 조절한다. [그림 3-31]의 1차시도에서는 인라이어가 세 개이고 2차 시도는 여섯 개이므로 1차는 버려질 가능성이 2차보다 높다. 모든 인라이어를 가지고 모델을 다시 추정한다. 2차 시도의 경우 여섯 개의 인라이어를 가지고 직선의 방정식을 다시 추정한다. 이러한 시도를 충분히 반복한 후 그동안 얻은 적합 모델 중에서 가장 좋은 것을 최종 답으로 취한다. 반복 회수는 [알고리즘 3-8]에서 n이라는 매개변수로 조절한다.

    
    //알고리즘 3-8 직선 검출을 위한 RANSAC
    //입력 : 에지 영상 e(j,i), 0 ≤ j ≤ M-1, 0 ≤ I ≤ N-1 // 에지는 1, 비에지는 0인 이진영상
    //반복 횟수 n, 인라이어 판단 t, 인라이어 집합의 크기 d, 직선 적합 오차 e
    //출력 : 하나의 직선(기울기 a와 절편 b)
    1  line=Φ;
    2  for(loop=1 to n) {
    3    에지 화소 두 개를 임의로 선택한다.
    4    이 두 점으로 직선의 방정식 l을 계산한다.
    5    이 두 점으로 집합inlier를 초기화한다.
    6    for(이 두 점을 제외한 모든 에지 화소 p에 대해)
    7      if(p가 직선 l에 허용오차 t이내로 적합) p를 inlier에 넣는다.
    8    if(|inlier|>=d) { // 집합 inlier가 d개 이상의 샘플을 가지면
    9      inlier에 있는 모든 샘플을 가지고 직선의 방정식 l을 새로 계산한다.
    10    if(l의 적합 오차 < e) l을 집합 line에 넣는다.
    11    }
    12 }
    13 line에 있는 직선 중 가장 좋은 것을 취한다.
     
  

3행은 에지 화소를 임의로 선택하고 있는데, 에지 강도와 에지 방향을 추가로 사용한다면 성능을 높일 수 있다. 예를 들어, 에지 강도가 높은 화소와 에지방향이 비슷한 화소 쌍이 선택될 가능성을 높이는 방안을 사용할 수 있다. 9행은 inlier의 샘플을 가지고 직선 l을 구한다. 예를 들어 [그림 3-31]의 2차 시도에서는 inlier는 여섯 개의 샘플을 가지며 이들로부터 구한 직선을 보여준다. 이때 샘플들이 정확히 l상에 존재하지 않으므로 적합오차가 발생한다. 10행은 이 적합 오차가 임계값보다 큰 경우 l을 버린다. 13행은 가장 좋은 직선을 최종 선택하는 과정인데, 좋은 정도를 판단하는 기준을 세워야 한다. 집합 inlier의 크기가 클수록 그리고 직선 l의 적합 오차가 작을수록 신뢰도가 높으므로 이 두기준을 가지고 좋은 정도를 측정하는 함수를 작성하면 된다. 여러 개의 직선을 찾고 싶다면 알고리즘을 적절히 수정해야한다. 한 가지 방법은 한번 수행한 후, inlier에 속하는 샘플들을 제외하고 같은 과정을 반복 하는 것이다.

출처 - Computer Vision