Hough Transform

Hough Transform

[알고리즘3-6]은 어떤 화소의 이웃을 조사하는 지역 연산local opration임에 비해, 허프 변환은 전체공간을 조사하는 전역 연산global operation이다. 또한 사람이 일직선 상에 있다고 지각하는 점들을 한 곳으로 모으는 원리를 사용하므로 일종의 지각 군집화perceptual grouping라고 볼 수 있다.

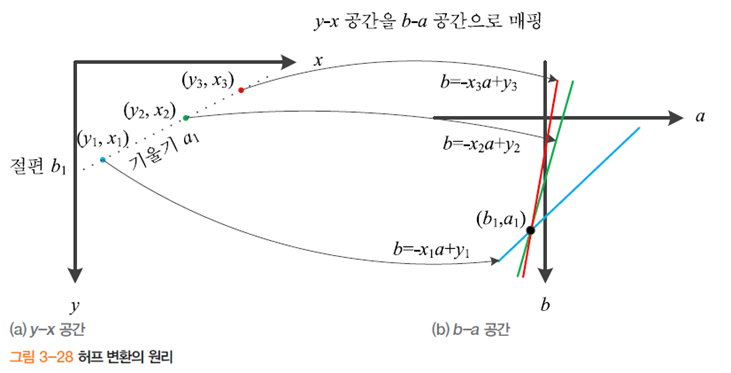
영상 공간(y-x공간)에 있는 각각의 에지 점(yi,xi)에 대해 b=-xia+yi 방정식의 자취를 b-a공간에 그린다. b-a공간에서 자취가 짙은 점 (bj, aj)를 추출한다. 이 점은 y-x공간에서 y=ajx+b라는 직선이다.

허프 변환을 구현할 때에 신중히 다뤄야하는 사항. 첫째, 수직선의 기울기 처리. 앞에서 직선의 방정식으로 y=ax+b를 사용했는데 y-x공간에서 수직선은 기울기가 무한대가 되므로 문제가 발생한다. 이 문제는 식(3.16)을 직선의 방정식으로 삼으면 간단히 해결된다. 이식의 그래프는 [그림3-29]와 같다.

\(\textcolor{Black}{ ycosθ+xsinθ=ρ (3.16) }\)

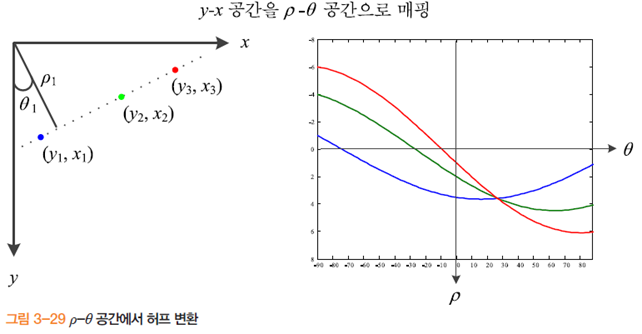
두 번째 고려할 사항은, [그림 3-29]에서는 세 점이 완벽하게 동일한 직선 위에 놓여 있다고 가정하였는데 실제 세계에서는 그렇지 못하다는 점이다. 특히 이산 공간에 에지 점이 정의되므로 어느 정도의 오류는 필연적으로 발생한다. 허프변환은 오류를 견디기 위해 ρ-θ공간을 적절한 구간으로 양자화한다. 그러면 오류를 흡수와 그래프의 자취가 밀집하는 곳을 용이하게 찾을 수 있는 효과도 있다. θ와 ρ가 가질 수 있는 범위는 각각 -90≤θ≤=90와 -D≤ρ≤D이다. D는 y-x공간의 원점에서 맞은편 꼭지점까지 거리이다. 이 범위를 적당한 구간으로 양자화 하여 얻은 2차원 배열 A를 누적 배열accumulation array 이라 부른다.

    
    //알고리즘 3-7 직선 검출을 위한 허프 변환
    //입력 : 에지 영상e(j,i), 0≤j≤M-1, 0≤i≤N-1, 임계값 T // 에지는 1, 비에지는 0인 이진 영상
    //출력 : (ρk,θk), 1≤k≤n(n개의 직선)
    1  2차원 누적 배열 A를 0으로 초기화 한다.
    2  for(에지 영상 e에 있는 에지 화소 (yi,xi)각각에 대해)
    3      yicosθ+xisinθ=ρ가 지나는 A의 모든칸을 1만큼 증가시킨다.
    4  A에서 T를 넘는 지역 최대점(ρk,θk)를 모두 찾아 직선으로 취한다.
    
  

허프 변환은 방정식으로 표현할 수 있는 어떠한 도형이라도 검출할 수 있다. 예를 들어 식 (3.17)은 중심이 (b,a)이고 반지름이 r인 원을 표현한다. 원을 거출하는 알고리즘은 직선을 검추하는 [알고리즘 3-7]을 약간 개조하면 된다. 이제 매개변수가 a,b,r세개이므로 누적배열 A가 2차원이 아니라 3차원이다.

허프 변환은 방정식으로 표현할 수 없는 임의의 모양을 가진 물체도 검출할 수 있다. 이에 대해서는 [Ballard82, 4장]을 참고하기 바란다. 이 책은 pdf파일로 공개되어 있다. http://homepages.inf.ed.ac.uk/rbf/BOOKS/BANDB/

출처 - Computer Vision