회전 공식 및 직선의 기울기

회전 공식

좌표 평면 점 P(x,y)를 각도 0만큼 회전시켜 P’(x’,y’)으로 옮기는 변환.

\[\textcolor{Black}{ {\begin{pmatrix}x' \\ y'\end{pmatrix}} = {\begin{pmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{pmatrix}} {\begin{pmatrix} x \\ y \end{pmatrix}} }\]

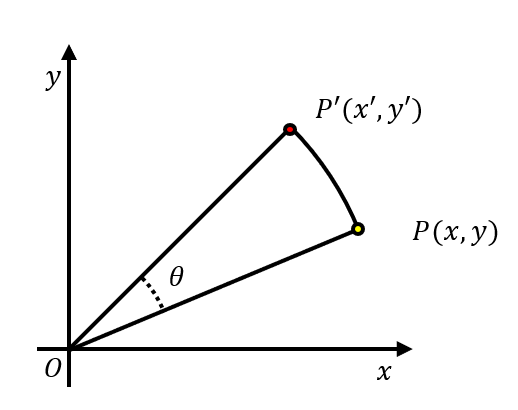
행렬을 각 요소에 대해 정리하면 다음과 같다.

\[\textcolor{Black}{ x' = xcos\theta - ysin\theta \\ y' = xsin\theta + ycos\theta }\]

직선의 기울기

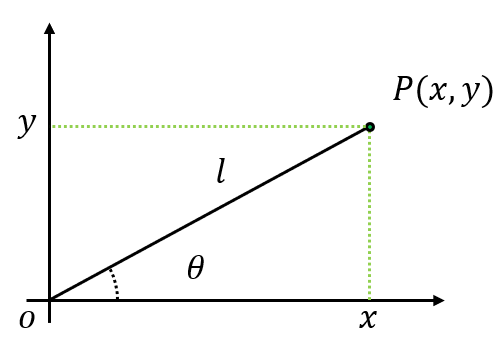
\(\textcolor{Black}{y=Ax+B}\) 일 때, 직선의 기울기는 다음과 같다.

\[\textcolor{Black}{ A = \frac{\Delta Y}{\Delta X} }\]

알고리즘 구현시 문제점이 발생하는데, \(\textcolor{Black}{\Delta X}\)가 0일 때, 예외처리를 해야한다.

이걸 회피 하기 위해 극좌표계를 이용하여 기울기를 \(\textcolor{Black}{\theta (Radian)}\)로 대치한다.

\[\textcolor{Black}{ l = \sqrt{\Delta X ^2 + \Delta Y ^2}\\ sin\theta = \frac{\Delta Y}{l} \\ \theta = arcsin(\frac{\Delta Y}{l}) }\]

다음과 같이 정의하여 사용할 때의 장점은 좌표에 대하여 분모가 0이 되지 않으므로 추가 예외처리가 필요 없다. 하지만 직선을 그리거나 좌표를 구할때는 결국 기울기로 바꿔야 하기때문에 추가 연산이 필요하다.

\[\textcolor{Black}{ A = \frac{\Delta Y}{\Delta X} = tan\theta }\]