이동과 회전에 불변한 특징점
모라벡(Moravec) 알고리즘
- 제곱차의 합 SSD(sum of squard difference)
\(\textcolor{Black}{f(.,.)}\) 는 입력 영상이고 \(\textcolor{Black}{w(.,.)}\)는 마스크이다. 현재 처리 중인 화소가 수식에 명시적으로 나타나지 않는다. 마스크 \(\textcolor{Black}{w(y,x)}\)는 (암시적으로 정해져 있는) 현재 화소를 중심으로 실제 계산에 참여할 곳을 지정한다. \(\textcolor{Black}{w(y,x)}\)는 현재 화소에 씌운 박스형 마스크인데, 박스 내의 화소는 1, 그 외의 모든 화소는 0을 갖는다. 박스 내의 화소에 대해서만 계산을 하는 셈이다. 컨볼루션은 현재 화소에서 한 개의 값만 생성하는 반면, 위 식은 (v,u)를 변화시켜가며 마스크 화소 각각에 대해 값을 생성한다. 따라서 [그림 4-3(b)]와 같이 S(v,u)라는 맵이 만들어진다.
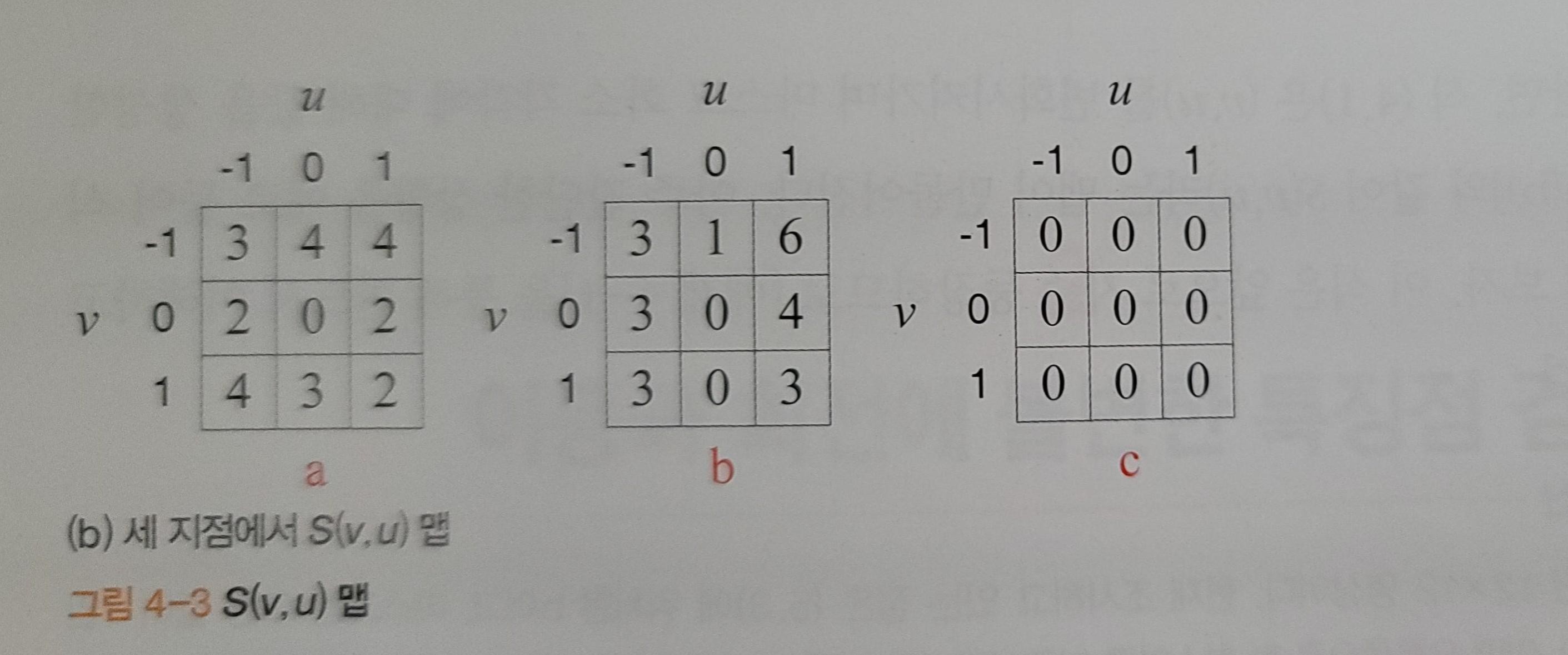
만일 현재 조사 중인 화소가 c와 같이 변화가 없는 곳인 경우, (v,u)를 변화시키며 주위를 조사하면 S(v,y)는 어느 방향으로든 낮은 값을 갖는다. 화소 c는 변화가 전혀 없으므로 아홉 개의 요소 모두 0을 갖는다. 이제 경계에 위치한 b를 살펴보자. 이곳의 에지는 세로 방향인데 그 방향으로는 낮은 값을 갖는 반면, 에지와 수직인 가로 방향으로 큰 값을 갖는다. 물체의 코너에 해당하는 a는 모든 방향에서 큰 값을 갖는다. 즉, 제곱차의 합이라는 함수 S는 어떤 점이 다른 곳과 얼마나 두드러지게 다른지 측정해 주는 역할을 한다. 물체의 코너는 두드러지게 다른 곳이므로 S를 코너일 가능성 정보로 해석할 수 있다.
모라벡은 [예제 4-1]과 같이 3x3 크기의 박스형 마스크를 사용하였으며, 동서남북 네 방향으로 한 화소만큼 이동시켜 얻은 네 개의 값 즉 (S(0,1), S(0,-1), S(1,0), S(-1,0))만 사용하였다. 그는 어떤 점이 코너라면 네 방향 모두 변화가 커야 한다고 보고, 네 값의 최솟값을 지역 특징일 가능성 값으로 간주하였다. 식 (4.2)는 모라벡이 정의한 ‘특징 가능성’ 값이다.
\[\textcolor{Black}{C=min(S(0,1),S(0,-1),S(1,0),S(-1,0))}\]해리스(Hariss) 코너
그는 잡음에 대처하기 위해 식(4.1)의 박스형 마스크를 중심에서 멀어질수록 서서히 값이 작아지는 가우시안 마스크 G(y,x)로 대치하였다. 이렇게 하여 식 (4.1)의 제곱차의 합은 식 (4.3)의 가중치 제곱차의 합WSSD(Weighted Sum Of Squared Difference)으로 확장 된다.
\[\textcolor{Black}{ S(v,u)=\sum_{y}\sum_{x} G(y,x)(f(y+v,x+u)-f(y,x))^{2} }\]가장 중요한 문제는 (v,u)를 어떻게 변화시켜 주위를 조사할 것인지에 관한 것이다. 모라벡은 한 화소만 이동시켜 동서남북을 조사하였다. 하지만 이렇게 하면 360˚ 모든 방향을 동등하게 취급한다는 등방성을 만족하지 못한다. 결국 물체가 0˚, 90˚, 180˚, 270˚ 만큼 회전하면 적절히 대처할 수 있지만 32˚나 48˚와 같이 임의의 값만큼 회전하는 경우는 대처하지 못한다. 다시말해 등방성을 만족하지 못해 매우 제한적인 회전 불변성을 지닌다는 뜻이다. 미분을 도입하면 이 문제를 해결할 수 있다. 테일러 확장Taylor expansion에 따르면 식 (4.4)가 성립한다.
(y,x)로 부터 작은양 (v.u)만큼 이동한점 (y+v, x+u)의 함수값 f(y+v, x+u)는 (y,x)에서 함수값 f(y,x)에 두 방향으로의 증가량인 vdy(y,x)와 udx(y,x)를 더해 준 값으로 근사화 할 수 있다는 뜻.
여기에서 dy(y,x)와 dx(y,x)는 (y,x)에서 도함수 ∂f/∂y 와 ∂f/∂x 의 값을 말한다. 해리스의 논문에서는 이들을 구하기 위해 y방향 마스크 [-1 0 +1]T와 x방향 마스크 [-1 0 +1]을 사용한다.
\[\textcolor{Black}{ f(y+v,x+u)≅f(y,x)+vd_y(y,x)+ud_x(y,x) (4.4) }\]식 (4.4)를 식 (4.3)에 대입한 후 정리하면 식 (4.5)를 얻는다.
\[\textcolor{Black}{ S(v,u)≅\sum_{y}\sum_{x} G(y,x)(vd_y(y,x)+ud_x(y,x))^2 (4.5) }\] \[\textcolor{Black}{ d_y (y,x)=d_y , d_x (y,x)= d_x }\] \[\textcolor{Black}{ =\sum_y\sum_xG(y,x)(v^2d_y^2+2vud_y d_x+u^2d_x^2) }\] \[\textcolor{Black}{ =\sum_y\sum_xG(y,x)(vd_y+ud_x )^2 }\] \[\textcolor{Black}{ =\sum_y\sum_x G(y,x)(v,u) \begin{pmatrix} d_y^2 & d_y d_x\\ d_y d_x & d_x^2 \end{pmatrix} \begin{pmatrix} v \\ u \end{pmatrix} }\] \[\textcolor{Black}{ = \begin{pmatrix} v\\ u \end{pmatrix} \sum_y\sum_x G(y,x)(v,u) \begin{pmatrix} d_y^2 & d_y d_x\\ d_y d_x & d_x^2 \end{pmatrix} }\] \[\textcolor{Black}{ S(v,u)≅(v,u)\begin{pmatrix} G * d_y^2 & G * d_y d_x \\ G * d_y d_x & G * d_x^2 \end{pmatrix} \begin{pmatrix} v \\ u \end{pmatrix} =uAu^T }\]
출처 - Computer Vision